行測數(shù)量關(guān)系空瓶換水的常見解題技巧
概念
空瓶換水，指的是給出n個空瓶可以換1瓶水的規(guī)則，問現(xiàn)有的空瓶最多可以換多少瓶水，或者要想喝到一定數(shù)量的水，問最少需要購買多少瓶水等類似的問題。
考法
1.直接套用規(guī)則：已知規(guī)則和空瓶數(shù)，求最多能喝到的瓶數(shù)
例1：一商店規(guī)定4個礦泉水空瓶可以換1瓶礦泉水，現(xiàn)有27個礦泉水空瓶，則最多可以換（ ）瓶礦泉水。
A.6 B.7 C.8 D.9
【答案】D【解析】當(dāng)?shù)V泉水瓶數(shù)量較小的時候，我們可以按規(guī)則一步一步地進(jìn)行兌換。但在實(shí)際考試過程中，這種方法不僅浪費(fèi)時間而且容易在兌換過程中出現(xiàn)差錯，這并不能滿足我們解決行測問題的快、準(zhǔn)原則。那我們該如何去計(jì)算呢？下面為大家提供一種更好的解題思路。
根據(jù)題干中的“4個礦泉水空瓶換1瓶礦泉水”，我們用等式來表示就可以寫成：4個礦泉水空瓶=1瓶礦泉水=1個礦泉水空瓶+1份水（一份水不包括空瓶），可以得：3個礦泉水空瓶=1份水。現(xiàn)在我們用27÷3=9，即27個礦泉水空瓶通過兌換最多可以得到9瓶水。答案選D。
總結(jié)：通過這個例題發(fā)現(xiàn)，在解決空瓶換水問題時，我們只需要找到空瓶與水的代換關(guān)系，即n個空瓶可以換1份水，然后用總的空瓶數(shù)m來除以n就可以得到最終答案。
2.間接套用規(guī)則：已知規(guī)則及喝到的瓶數(shù)，求至少應(yīng)買多少瓶水
例2：商店做活動，8個空瓶可以換一瓶水，小芳這個月一共喝了65瓶水，那么她花錢買的至少有多少瓶水？（ ）
A.56 B.57 C.58 D.59
【答案】B【解析】首先我們需要注意，小芳喝的這65瓶水包括小芳她自己花錢買的和通過兌換得到的。因此，如果我們設(shè)小芳花錢買了x瓶水，并且題干中的“8個空瓶可以換一瓶水”，我們用等式來表示可以寫成：8個礦泉水空瓶=1瓶礦泉水=1個礦泉水空瓶+1份水（一份水不包括空瓶），可以得：7個礦泉水空瓶=1份水。則小芳通過兌換可以得到x÷7瓶水，因此可以得到x+x÷7=65，解得x=56.875，即至少買56.875瓶水加上兌換的才能保證小芳這個月喝了65瓶，而礦泉水瓶數(shù)只能是整數(shù)，因此在不小于56.875的整數(shù)里選擇最小的57，答案選B。
總結(jié)：當(dāng)我們已知規(guī)則及喝到的瓶數(shù)，求至少應(yīng)買多少瓶水時，我們只需要利用換水規(guī)則列方程求解即可。只不過需要注意的是，當(dāng)未知數(shù)解出來為非整數(shù)時，我們需要向上取整。
基本原理
我們通過下面這一道題目來探究一下這類題目的通用解法。
例1：3個空啤酒瓶可以免費(fèi)換一瓶啤酒，現(xiàn)有32個啤酒空瓶，請問最多可以免費(fèi)喝多少啤酒（ ）？
A.13 B.14 C.15 D.16
【答案】D【解析】很多同學(xué)拿到這類題目，往往就是一步一步地去換：
第一步：32個空瓶可以拿出30個空瓶來換10瓶啤酒，還剩2個空瓶；
第二步：把這10瓶啤酒喝掉可以得到10個空瓶，那么就一共有12個空瓶，再拿去換4瓶啤酒；
第三步：把這4瓶啤酒喝掉可以得到4個空瓶，拿出3個空瓶換1瓶啤酒，這時還剩下1個空瓶；
第四步：把這1瓶啤酒喝掉可以得到1個空瓶，一共就有了2個空瓶。2個空瓶看似不夠換一瓶，但實(shí)則我們可以借1個空瓶過來，湊夠3個空瓶，換得1瓶啤酒喝掉后再把借來的這1個瓶子還掉就可以了。
這樣一共可以免費(fèi)喝10+4+1+1=16瓶，故選擇D選項(xiàng)。
但這個方法非常浪費(fèi)時間，而且最后這個瓶子是需要借的，很多同學(xué)想不到這點(diǎn)。所以為大家?guī)硪环N更快解題的方法：
解析：根據(jù)題意3個空瓶=1瓶啤酒，我們可以把這1瓶啤酒看成1個空瓶加1份酒，得到3個空瓶=1個空瓶+1份酒，那么等式兩邊的1個空瓶可以消掉，變成2個空瓶=1份酒，也就是有2個空瓶就可以喝1份酒，那么32個空瓶就可以喝32÷2=16瓶酒，故選擇D項(xiàng)。
【模型特征】：已知兌換規(guī)則及空瓶數(shù)，求最多能喝到的瓶數(shù)。
【基本公式】：假設(shè)n個空瓶可以換一瓶水，那么m個空瓶最多可以喝到m÷（n-1）瓶水。
靈活考法
為了讓大家能夠更好地掌握這類題型，我們再一起來了解一下它常見的變形。
例2：某啤酒開展“12個空瓶換1瓶啤酒”的大型促銷活動，小張和他朋友在活動期間共喝了245瓶啤酒，那么他們至少需要買多少瓶啤酒？（ ）
A.223 B.224 C.225 D.226
【答案】C【解析】根據(jù)題意小張和他朋友喝的245瓶啤酒包括了花錢買的和通過兌換得到這兩部分。因此這道題本質(zhì)上還是空瓶換水的思路：將一瓶啤酒看成1個空瓶+1份酒，所以根據(jù)兌換規(guī)則得到12空瓶=1空瓶+1份酒，也就是11空瓶=1份酒，設(shè)買了x瓶水，可得：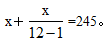
解得想x≈224.6，因?yàn)閤為正整數(shù)且最少為224.6，所以n向上取整為225，故選擇C項(xiàng)。
通過這道題可以得到空瓶換水問題的變形總結(jié)：已知兌換規(guī)則及喝到的水?dāng)?shù)，求至少買多少瓶。這類題目只需要利用兌換規(guī)則列方程求解即可。值得注意的是當(dāng)未知數(shù)解出來為非整數(shù)時，記得取整。
例題3：若5個礦泉水空瓶可以免費(fèi)換1瓶礦泉水，現(xiàn)有132個礦泉水空瓶，最多可以免費(fèi)喝到幾瓶礦泉水？（ ）
A.31瓶 B.32瓶 C.33瓶 D.34瓶
【答案】C【解析】拿到這道題，很多同學(xué)估計(jì)已經(jīng)開始在草稿紙上演算了，一步一步地去換水。先拿132個空瓶去換水，可以換132÷5=26…….2，即換26瓶水且余2個空瓶；26瓶水喝完又有26個空瓶，和之前剩余的2個空瓶此時共有28個空瓶。28個空瓶又可以換28÷5=5……3，即換5瓶水且余3個瓶子；以此類推，8÷5=1……3，此時喝完1瓶水得到1個空瓶，加上剩余的3個空瓶，一共有4個空瓶，到這一步有同學(xué)就想手里的瓶子已經(jīng)不夠換水了，那么一共喝到了26+5+1=32瓶。遺憾的是，經(jīng)過這樣一步一步繁瑣的過程最終還是做錯了，實(shí)在可惜。
為什么呢？這樣思考本身沒有問題，但是易錯的地方是最后4個空瓶能否換水呢？此時差一點(diǎn)就可以換到水了，不換豈不有點(diǎn)可惜？那能否想辦法換到呢？就差一個空瓶而已，試想一下，我們可否借一個空瓶，那么我們就湊齊了5個空瓶，此時便可換到1瓶水，喝完有1個空瓶，正好可以還回去，兩全其美，何樂而不為呢？這樣一想，我們完全還可以再喝到1瓶水的，所以我們最多可以喝到33瓶水，正確答案應(yīng)該選C項(xiàng)。
經(jīng)過上面這樣一步步地思考兌換的過程，我們不難發(fā)現(xiàn)，這樣去做空瓶換水類的題目太過繁瑣，而且一不小心容易出錯，那么有沒有技巧可以幫助我們避免錯誤，而且能快速做對類似的題目呢？肯定是有的。實(shí)際上，我們根據(jù)題干中的交換規(guī)則“5個空瓶子換1瓶水”，可得“5空瓶=1瓶水=1空瓶+1份水”，化簡為“4空瓶=1份水”，所以最多能免費(fèi)喝到132÷4=33瓶水，故選擇C選項(xiàng)。
結(jié)論：若n個空瓶換1瓶水，則n-1個空瓶=1份水。
例題4：某啤酒廠為促銷啤酒，開展6個空啤酒瓶換1瓶啤酒的活動，孫先生去年花錢先后買了109瓶該品牌啤酒，期間不斷用空啤酒瓶去換啤酒，請問孫先生去年一共喝掉了多少瓶啤酒？（ ）
A.127瓶 B.128瓶 C.129瓶 D.130瓶
【答案】D【解析】根據(jù)題干信息，6個空瓶=1個空瓶+1份啤酒，則5個空瓶=1份啤酒，孫先生買了109瓶該啤酒，也就有109個空啤酒瓶，因此109個空啤酒瓶最多可以換到啤酒109÷5=21.X瓶，所以孫先生去年一共喝掉109+21=130瓶啤酒，故本題選D。
通過上面兩道題目，大家不難發(fā)現(xiàn)空瓶換水類題目易掌握、易得分，每位同學(xué)都可以快速掌握，只要考到了，直接套用公式就可以輕松解決。
空瓶換水里的數(shù)學(xué)思維
例1：某商店節(jié)日促銷，以“回收環(huán)保，以3換1”的主題售賣飲料。具體規(guī)定如下：3個同款飲料空瓶可以免費(fèi)換1瓶同款飲料。一瓶飲料售價5元。李紅現(xiàn)有30元，最多可以喝到幾瓶飲料？（ ）
A.9 B.8 C.6 D.10
【答案】A【解析】易錯點(diǎn)：李紅首先可以用30元買6瓶飲料，喝完飲料以后得到6個空瓶。這6個空瓶還可以換2瓶飲料，再喝完會剩下2個空瓶，不滿足“以3換1”的條件。所以一共可以喝到8瓶飲料。選擇B項(xiàng)。但這并不是最優(yōu)方案，為什么呢？
思路一：其實(shí)大家忽略了一種情況，李紅可以先向商店“借”1個空瓶，這樣加上之前剩下的2個空瓶，就湊夠了3個空瓶，再去換一瓶飲料喝掉，最后把喝掉剩下的空瓶還給商店，能夠達(dá)到“借1還1”的狀態(tài)。這種數(shù)學(xué)思維能夠達(dá)到最多喝9瓶飲料的結(jié)果。選擇A項(xiàng)。
思路二：思路一可以達(dá)到最多的情況，但是只限數(shù)值較小的題目，如果這道題變成李紅有100元，甚至更多錢，一點(diǎn)一點(diǎn)的推理會非常耗費(fèi)時間，同時還需要考慮剩下的瓶子、換了以后的瓶子、借瓶子的情況等等。所以接下來的方法才是大家學(xué)習(xí)的重點(diǎn)。
最終我們需要的是最多能喝多少瓶飲料，所以可以從替換關(guān)系入手分析。3個空瓶=1瓶飲料→3個空瓶=1個空瓶+1份飲料（沒有瓶子裝的飲料）→2個空瓶=1份飲料。這樣的替換關(guān)系就可以忽略再次換飲料以后還會留下空瓶的過程。現(xiàn)在李紅有30元，可以先買30÷5=6瓶飲料，得到6份飲料和6個空瓶，替換關(guān)系為2個空瓶=1份飲料，所以其中的6個空瓶=3份飲料，最終最多可以喝到6+3=9份飲料。選擇A項(xiàng)。
例2：某商店節(jié)日促銷，以“回收環(huán)保，以5換1”的主題售賣飲料。具體規(guī)定如下：5個同款飲料空瓶可以免費(fèi)換1瓶同款飲料。一瓶飲料售價5元。李紅現(xiàn)有100元，最多可以喝到幾瓶飲料？
A.20 B.24 C.25 D.26
【答案】C【解析】5個空瓶=1瓶飲料→5個空瓶=1個空瓶+1份飲料（沒有瓶子裝的飲料）→4個空瓶=1份飲料。現(xiàn)在李紅有100元，可以先買100÷5=20瓶飲料，得到20份飲料和20個空瓶，替換關(guān)系為4個空瓶=1份飲料，所以其中的20個空瓶=5份飲料，最終最多可以喝到20+5=25份飲料。選擇C項(xiàng)。
如何巧解此類題目
例1：某商店為了吸引顧客做一個促銷活動，每3個空汽水瓶可以換一瓶汽水，問：小張共有11個空瓶最多可以喝到幾瓶汽水？（ ）
【解析】（1）基本方法：由于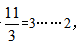
可知能換到3瓶汽水還剩2個空瓶，3瓶汽水喝掉后再加剩余的2個空瓶，可得到5個空瓶。
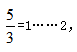能換到1瓶汽水還剩2個空瓶，1瓶汽水喝掉可得到3個空瓶，又能換到1瓶汽水，最終共喝到3+1+1=5瓶汽水。
（2）巧解方法：明確題目中的核心兌換規(guī)則，3個空瓶換1瓶汽水，也就是3空瓶=1瓶水=1空瓶+1份水，即2空瓶=1份水。因此，直接用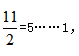
最多能喝到5瓶汽水。
【解題方法】直接套用公式——已知規(guī)則及空瓶數(shù)，問最多能喝到水的瓶數(shù)。
例2：若12個空瓶可以免費(fèi)換1瓶汽水，現(xiàn)有101個空瓶，最多可以免費(fèi)喝到幾瓶汽水？
A.8瓶B.9瓶C.10瓶D.11瓶
【答案】B【解析】明確題目中的兌換規(guī)則，12個空瓶換1瓶水，即12空瓶=1瓶水=1空瓶+1份水，即11空瓶=1份水。因此所求為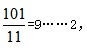
最多能喝到9瓶汽水。
例3：商店開展“7個空瓶換一瓶啤酒”的優(yōu)惠活動。已知張先生在活動促銷期間共喝掉347瓶“紅星”啤酒，問張先生最少買多少瓶啤酒？（ ）
A.296 B.298 C.300 D.302
【答案】B【解析】明確題目中的兌換規(guī)則，7空瓶=1瓶酒=1空瓶+1份啤酒，即6空瓶=1份啤酒。此時設(shè)張先生最少需要買x瓶啤酒，則換回酒的份數(shù)為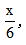
由題可得：
此時需要分析x的取值，x假設(shè)為最少，而啤酒的瓶數(shù)一定是整數(shù)，需要向上取整，因此最少需要買298瓶啤酒，故選擇B選項(xiàng)。
【解題方法】間接套用公式——已知規(guī)則及喝到水的份數(shù)，求至少應(yīng)買多少瓶水。
以上即為空瓶換水的巧解方法。以后解決此類問題時，首先需要明確題目中的兌換規(guī)則，將兌換規(guī)則轉(zhuǎn)化為a空瓶=b份水的形式，再進(jìn)行求解即可。此類問題在考試中的考查形式相對來講比較單一，同學(xué)們只要明確方法，相信可以輕松解決。
