
行測(cè)數(shù)量關(guān)系答題技巧:淺談“植樹(shù)問(wèn)題”
大家在公務(wù)員行測(cè)數(shù)量關(guān)系考試中,可能經(jīng)常會(huì)遇到這樣的問(wèn)題:張亮的房間在賓館18層,從第1層乘電梯到他所住的樓層要34秒,李林住在31層,從張亮所住的樓層乘電梯到31層要用()秒。對(duì)于這樣的題目可能很多同學(xué)都會(huì)出錯(cuò),今天我們就針對(duì)這種問(wèn)題進(jìn)行了劃類(lèi),這種問(wèn)題就是我們接下來(lái)要說(shuō)的“植樹(shù)問(wèn)題”,下面我們就來(lái)進(jìn)行一下簡(jiǎn)要的歸納和闡述。
什么是植樹(shù)問(wèn)題?
植樹(shù)問(wèn)題是在一定的線路上,根據(jù)總路程、間隔長(zhǎng)和棵數(shù)進(jìn)行植樹(shù)的問(wèn)題。
常見(jiàn)題型
(一)路不封閉且兩端植樹(shù)問(wèn)題:棵樹(shù)=總路長(zhǎng)÷間距+1.
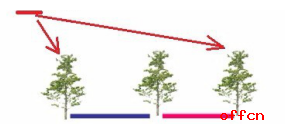

圖中有2段路,3棵樹(shù),栽樹(shù)的棵樹(shù)比路的段數(shù)多1。
例1:有一條堤全長(zhǎng)500米,從頭到尾每隔5米種植白楊樹(shù)一棵,一共可以種( )棵。
A.100
B.101
C.99
D.102
解析:兩端植樹(shù)問(wèn)題。已知每隔5米植樹(shù)一棵,則一共可以種500÷5+1=101棵樹(shù)。
(二)路不封閉且一端植樹(shù)問(wèn)題:棵樹(shù)=總路長(zhǎng)÷間距.

圖中有2段路,2棵樹(shù),栽樹(shù)的棵樹(shù)與路的段數(shù)相等。
例2:從紀(jì)念塔到電影院的路上共有1000米,每隔10米放一盆花,問(wèn)總共可以放多少盆?( 紀(jì)念塔下有1盆,電影院門(mén)口沒(méi)有)
解析:路不封閉且一端植樹(shù)問(wèn)題。根據(jù)公式可得,一共有1000÷10=100盆。
(三)路不封閉且兩端都不植樹(shù)問(wèn)題:棵樹(shù)=總路長(zhǎng)÷間距-1.

圖中有2段路,1棵樹(shù),栽樹(shù)的棵樹(shù)比路的段數(shù)少1。
例3:兩座樓之間相隔56米,每隔4米栽一棵樹(shù),問(wèn)一行能栽多少棵樹(shù)?
解析:路不封閉且兩端都不植樹(shù)問(wèn)題。因?yàn)闃?shù)只能在兩個(gè)樓的中間植,所以,樹(shù)的數(shù)目=56÷4-1=13棵。
(四)封閉空間植樹(shù)問(wèn)題:棵樹(shù)=總路長(zhǎng)÷間距.
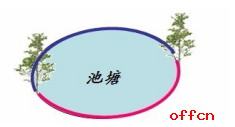
圖中有2段路,2棵樹(shù),栽樹(shù)的棵樹(shù)與路的段數(shù)相等。
例4:在一周長(zhǎng)為50米的花壇周?chē)N樹(shù),如果每隔5米種一棵,一共可以種( )棵。
A.10
B.11
C.12
D.15
解析:封閉空間植樹(shù)問(wèn)題。由題意可知,花壇周?chē)煞N50÷5=10棵樹(shù)。
以上就是我們“植樹(shù)問(wèn)題”的幾種常見(jiàn)的題型,需要值得大家注意的是:有的時(shí)候在行測(cè)理科考試過(guò)程中,并不是會(huì)直接給出我們這么明顯的植樹(shù)問(wèn)題,而是會(huì)進(jìn)行相應(yīng)的變形,比如說(shuō)鋸木問(wèn)題、上樓梯問(wèn)題、敲鐘問(wèn)題以及排隊(duì)問(wèn)題等各式各樣的變化形式。下面,咱們來(lái)看一道變形的“植樹(shù)問(wèn)題”吧~
例5:運(yùn)動(dòng)會(huì)上,接受檢閱的一列彩車(chē)車(chē)隊(duì)共52輛,每輛車(chē)長(zhǎng)4米,前后每輛車(chē)間隔6米,車(chē)隊(duì)每分行駛105米。這列車(chē)隊(duì)要通過(guò)536米長(zhǎng)的檢閱場(chǎng)地,需要多少分鐘?
A.4.9
B.8
C.10
D.10.1
解析:52輛車(chē)長(zhǎng)度為:52*4=208米,有52-1=51個(gè)間隔,車(chē)隊(duì)總長(zhǎng)為208+51*6=514米。通過(guò)536米長(zhǎng)的檢閱場(chǎng)地共需要行駛526+514=1050米,費(fèi)時(shí)1050÷105=10分鐘。
看完上面的簡(jiǎn)要分析大家就能知道,其實(shí)“植樹(shù)問(wèn)題”變化形式多樣,但是只要是“認(rèn)清它的廬山真面目”,計(jì)算起來(lái)還是相當(dāng)簡(jiǎn)單的!最后,我們祝愿大家都能成功上岸!
巧解植樹(shù)問(wèn)題
植樹(shù)問(wèn)題,考試頻率不算高,但也算是時(shí)有考察,這類(lèi)問(wèn)題考察難度不大,但考生總是容易出錯(cuò),主要考察我們的細(xì)心程度,接下來(lái),我們就帶大家一起來(lái)探索梳理一下關(guān)于這類(lèi)問(wèn)題的相關(guān)知識(shí)點(diǎn):
一、概念
按相等的距離植樹(shù),在距離、棵距、棵數(shù)這三個(gè)量之間,已知其中的兩個(gè)量,要求第三個(gè)量,這類(lèi)應(yīng)用題叫植樹(shù)問(wèn)題。
二、常用公式
1.線性植樹(shù)(兩端植樹(shù)) 棵數(shù)=距離÷棵距+1
2.環(huán)形植樹(shù) 棵數(shù)=距離÷棵距
3.方形植樹(shù) 棵數(shù)=距離÷棵距-4
4.三角形植樹(shù) 棵數(shù)=距離÷棵距-3
【注】植樹(shù)問(wèn)題的關(guān)鍵是要先分析題目弄清楚問(wèn)題的類(lèi)型,然后利用公式。
三、經(jīng)典例題
例1.一座大橋長(zhǎng)500米,給橋兩邊的電線桿上安裝路燈,若每隔50米有一個(gè)電桿,每個(gè)電桿上安裝2盞路燈,一共可以安裝多少盞路燈?
A.40 B.44 C.48 D.50
【解析】這是一道典型的線性植樹(shù)問(wèn)題,對(duì)應(yīng)的公式為:棵數(shù)=距離÷棵距+1,橋的一邊電線桿的數(shù)量為500÷50+1=11個(gè),那么兩邊電線桿有11×2=22個(gè),則大橋兩邊可安裝的路燈為22×2=44盞,故選答案B。
例2.李大爺在馬路邊散步,路邊均勻地栽著一行樹(shù),李大爺從第1棵樹(shù)走到第15棵樹(shù)共用了7分鐘,李大爺又向前走了幾棵樹(shù)后就往回走,當(dāng)他回到第5棵樹(shù)時(shí)共用了30分鐘。李大爺步行到第幾棵樹(shù)時(shí)就開(kāi)始往回走?
A.第32棵 B.第33棵 C.第37棵 D.第38棵
【解析】李大爺從第1棵樹(shù)走到第15棵樹(shù)一共走了15-1=14個(gè)間距,每個(gè)間距的時(shí)間為14÷7=2分鐘,剩下的23分鐘李大爺可以走23×2=46個(gè)間距,以第5棵樹(shù)為基準(zhǔn),往回走到第5棵樹(shù)比從第15棵樹(shù)走到回頭的地方要多走15-5=10個(gè)間距,即還能再向前走(46-10)÷2=18個(gè)間距,即走到第15+18=33棵樹(shù)時(shí)回頭,故選答案B。
例3.一個(gè)正方形的運(yùn)動(dòng)場(chǎng),每邊長(zhǎng)220米,每隔8米安裝一個(gè)照明燈,一共可以安裝多少個(gè)照明燈?
A.100 B.102 C.104 D.106
【解析】這是一道方形的植樹(shù)問(wèn)題,公式是:棵數(shù)=距離÷棵距-4,直接利用公式220×4÷8-4=110-4=106個(gè),故選答案D。
以上就是植樹(shù)問(wèn)題常考題型以及它的的變化形式,核心就是找到棵數(shù)與間距之間的關(guān)系,希望大家在理解的基礎(chǔ)上多加練習(xí),那么在考試當(dāng)中就可以得心應(yīng)手了!
行測(cè)數(shù)量關(guān)系常見(jiàn)考點(diǎn)解析:植樹(shù)問(wèn)題
植樹(shù)問(wèn)題屢屢出現(xiàn)在歷年事業(yè)單位考試中,雖然題目難度并不是很大,同時(shí)考生們也覺(jué)得這種題目很有意思,就是規(guī)律不好把握,所以學(xué)生容易出錯(cuò)。我們認(rèn)為,其實(shí)植樹(shù)問(wèn)題是有規(guī)律可循的,只要能夠掌握植樹(shù)問(wèn)題的相關(guān)公式,熟練運(yùn)用我們的解題方法,那么這種問(wèn)題肯定能夠輕松應(yīng)對(duì)。
一、認(rèn)識(shí)植樹(shù)問(wèn)題
植樹(shù)問(wèn)題屬于邊端計(jì)數(shù)問(wèn)題,首先問(wèn)大家一個(gè)問(wèn)題。一段繩子減成三段,需要減幾次?應(yīng)該是兩次。而植樹(shù)和這個(gè)問(wèn)題有點(diǎn)類(lèi)似,只不過(guò)需要考慮邊端是否計(jì)算的問(wèn)題。而邊端計(jì)數(shù)問(wèn)題是一種特殊的計(jì)數(shù)問(wèn)題,它是建立在幾何基礎(chǔ)之上,同時(shí)需要注意加減1的問(wèn)題,那么來(lái)看一下植樹(shù)問(wèn)題的模型公式:
植樹(shù)問(wèn)題包含單邊植樹(shù)與雙邊植樹(shù)兩種模型:
單邊線型兩端植樹(shù)公式:棵數(shù)=總長(zhǎng)÷間隔+1;總長(zhǎng)=(棵數(shù)-1)×間隔
單邊線型兩端不植樹(shù)公式:棵數(shù)=總長(zhǎng)÷間隔-1;總長(zhǎng)=(棵數(shù)+1)×間隔
單邊環(huán)型植樹(shù)公式:棵數(shù)=總長(zhǎng)÷間隔;總長(zhǎng)= 棵數(shù)×間隔
雙邊植樹(shù)公式=單邊植樹(shù)的顆數(shù)×2
二、試題解析
【例題】植樹(shù)節(jié)要到了,某學(xué)校購(gòu)買(mǎi)一批樹(shù)苗計(jì)劃在一段路兩旁植樹(shù)。若每隔5米種1棵樹(shù),可以覆蓋整個(gè)路段,但這批樹(shù)苗剩20棵。若每隔4個(gè)種1棵樹(shù)且路尾最后兩棵樹(shù)之間的距離為3米,則這批樹(shù)苗剛好可覆蓋整個(gè)路段。這段路長(zhǎng)為( )。
A. 195米 B. 205米 C. 375米 D. 395米
【答案】A
【解析】此題是一個(gè)雙邊植樹(shù)問(wèn)題:線型植樹(shù)問(wèn)題,先計(jì)算出單邊植樹(shù)的個(gè)數(shù),在此一邊棵樹(shù)的基礎(chǔ)上乘以2,就可以計(jì)算出雙邊植樹(shù)需要的樹(shù)木的個(gè)數(shù)。設(shè)路長(zhǎng)為x,則
,解x=195。
【例題】施工隊(duì)要在一東西長(zhǎng)600米的禮堂頂部沿東西方向安裝一排吊燈,根據(jù)施工要求,必須在距西墻375米處安裝一盞,并且各吊燈在東西墻之間均勻排列(墻角不能裝燈)。該施工隊(duì)至少需要安裝多少盞吊燈?
A.6 B.7 C.8 D.9
【答案】B
【解析】植樹(shù)問(wèn)題:根據(jù)題意, 兩個(gè)端點(diǎn)不能裝吊燈,就意味著是線型兩端不植樹(shù)模型,根據(jù)禮堂總長(zhǎng)600米,而在距西墻375米處必須安裝一盞,可算出每?jī)蓚€(gè)燈之間的間距為600及375的最大公約數(shù)75,則最后安裝了 ,故答案選擇B選項(xiàng)。
,故答案選擇B選項(xiàng)。
我們認(rèn)為,數(shù)學(xué)是一門(mén)技巧性很強(qiáng)的學(xué)科,它總是能夠利用各種巧妙的方式把復(fù)雜問(wèn)題簡(jiǎn)單化,這就是數(shù)學(xué)的神奇之處。相信通過(guò)大家對(duì)數(shù)的植樹(shù)問(wèn)題的學(xué)習(xí)和掌握,在參加接下來(lái)的事業(yè)單位考試中又可以巧妙的解決一個(gè)數(shù)量關(guān)系學(xué)習(xí)過(guò)程中的難點(diǎn)。祝愿各位同學(xué)都能在接下來(lái)事業(yè)單位考試中順利通過(guò)筆試!








